Preface (Toru
Nakagawa, Aug. 5, 2001)
One of the USIT's textbook problems, "The Picture Hanging Kit Problem" written by Dr. Ed Sickafus, was translated into Japanese and posted in this Web site on March 23, 2001. My intention was to introduce to Japanese readers a good case study of USIT with emphasis on how to use the solution generation methods in USIT. This case study is nice but rather voluminous, and the processes of generating a large number of solution concepts are complicated in the original text.Editor's Note (Toru Nakagawa, Aug. 23, 2001)For conducting a 3-day USIT Training Seminar on July 11-13 in Tokyo, I prepared about 35 slides on this case study to explain the USIT process in my own words. During this preparation and during the discussions at the seminar, I could understand this case study much more deeply and obtained some new insights into USIT itself.
Hence, by using and enhancing the slides, I have written an article here (first in Japanese and then in English translation) for explaining Sickafus' "Picture Hanging Kit Problem" and for mentioning my understandings and comments. Please refer to the original description by Sickafus in his USIT Textbook (1997), and some of my introductory articles on USIT in this Web site. I hope this article useful for readers to understand the actual process in our mind while our applying USIT to technical problem solving.
Dr. Ed Sickafus, on his reading my draft of this article, kindly sent me his message on August 13, 2001 as follows:Toru, thanks for sharing your work with me. I'm very impressed. I believe there is no better way to learn a subject than to teach it. In the case of USIT, preparing all of the slides for a USIT demonstration is always a fruitful exercise and always has surprises. My comments on your text and pictures are in the attached Word file.Under his permission, I have inserted his discussions into their relevant places in this article with ** marks and in blue texts. Two views, sometimes placing emphasis on different points, may be helpful for readers to understand USIT more deeply.
With best regards, Ed
| Top of this page | 1. Problem Definition | 2. Problem Analysis | 3. Solution Generation | Introduction to USIT (Nakagawa, Apr. 2000) | Japanese
page |

(1) The slides and explanations of this article were written by Toru Nakagawa in order to study Ed Sickafus' Textbook problem, i.e. "The Picture Hanging Kit Problem". The description here follows the problem solving procedure with USIT. Please refer Ed Sickafus' USIT Textbook for the original source of the full description of this problem. [Sickafus' text of this problem was translated into Japanese and posted earlier in March 2001 in this "TRIZ Home Page in Japan" under author's permission.] This problem was originally written as Appendix E9 in the 488-page USIT Textbook. Sickafus once gave a lecture on USIT towards high-school science students with this example and wrote it down with some enhancement, as we can see now. |

(2) "Problem Situation" shows the initial situation of the problem, and explains the stage just before starting to solve the problem. In industries, an abstract direction like the one shown in this slide is often decided by top management, managers, planning division, etc. and is given to relevant technologists. In other cases, a problem recognition like this arises inside the technology group, and is talked or written down to explain the present situations in problem before starting to solve it. The team who get in charge of solving a problem should first of all understand (often by interviewing) the "Problem Situation" correctly. If the team fails to understand the situation properly, all their subsequent efforts for problem solving will become useless. |
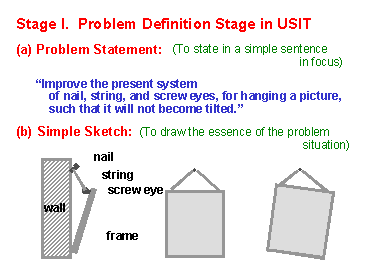
(3) Now we start the problem solving process with USIT. USIT shows us a clear guideline what and how we should think all through the way of problem solving. In the first stage, i.e. Problem Definition Stage in USIT, the team needs to clarify what is the problem to solve, on the basis of the Problem Situation mentioned above. The team sometimes may be able to clarify the problem through their former experiences and their discussions, but more often they need information, data, and technological explanations from the people relevant to the problem. This slide is an example obtained and summarized through such a process of clarification. We should make a simple summary of problem definition as shown in this slide. USIT advises to formulate a "Problem Statement" as concise as one or two lines. Conciseness is the key to ensuring clarity. Making a sketch is important to consider the mechanism of the problem. ** |
** [Discussion by Sicakfus:]Making a sketch of objects forces one to establish a clearer understanding of the objects and their interactions.

(4) Then we should reveal plausible root causes of the problem. This task is equivalent to understanding the mechanism of the problem. Dr. Sickafus is an experimental physicist and has been working in academia and in industries (Ford Motor Company) and have achieved a lot. On the basis of his profound background in physics, he advises us to make deep understanding and insights into the mechanisms of problems. For such understanding of mechanism, rather than theoretical or quantitative treatment, usually more important is to understand the causal relationships among phenomena. He puts stress on "phenomenological analysis" in such a sense. ** This slide shows Sickafus' process to reveal "the mechanism of the problem" in the present case. |
** I would call a phenomenological analysis a theoretical analysis without equations and an experimental analysis without numbers.
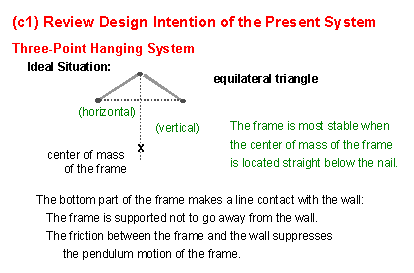
(5) As the first step to reveal the mechanism, we should review the intention in the original design of the present system. For doing so, we consider the ideal case where the situation is just as expected. When we hang something, it is most important to consider where its center of mass is located. Even though we consider phenomenologically, we should not just say something like "to hang it right" but talk with the words in basic physics. The contact relation of the bottom part of the frame with the wall is also mentioned, and the six degrees of freedom are discussed for locating a frame (i.e., three translational and three rotational degrees). |
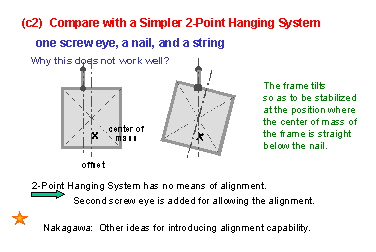
(6) In the previous slide we confirmed the importance of locating the center of mass of the frame right below the nail. Then, after recognizing that such a location can be more easily achieved just by hanging the frame with one screw eye, Sickafus analyzes the simpler two-point hanging system. In this simpler system, if the position of the screwy (or the hook) is offset, the frame is hung tilted; and there is no way of readjusting it. For the purpose of introducing a means of readjusting the tilt, the second screw eye is used; this confirms the intention of the present three-point hanging system. Even though Dr. Sickafus does not mention here, the figure in this slide gives us a hint for introducing another way of readjusting the tilt; namely to adjust the location of the screw eye (or the hook), as is shown later. As clear in this example, if one draws a sketch of any situation or idea, one can often be stimulated with another idea. ** |
** This is an excellent point to drive home.
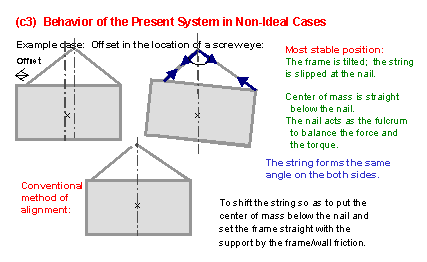
(7) We now come back to the present three-point hanging system and examine the behavior of the system in non-ideal cases where the frame is hung with some kind of offset and misalignment. The upper right figure shows the situation when the frame is hung with a tilt due to some offset in the position of one screwy. In the most stable position of the frame, "the two parts of the string form the same angles with the vertical line". This conclusion is obtained by Nakagawa and is clearer than Sickafus' explanation shown with the vertical and horizontal components of the forces. The tension on the string is the same everywhere, and the forces and the torques onto the frame are balanced under this condition. Even if there is an offset in the position of the screw eye, one can often hang the frame at the right alignment with a practical trick. You may set the frame as is drawn in the bottom figure and leave it softly on the wall. If the friction between the frame and the wall is large enough, the frame will stay in its position for some time. When a vibration from the wall is given to the frame, or when something hits on the frame, this frame will tilt to get into the most stable position as shown in the upper right figure. |

(8) Next we should list up the objects in the present system. First, at the upper part, we have listed up as many objects as possible as the candidates for analysis. Then we should reduce them into the minimal set of objects directly relevant to the present problem, i.e. the problem of hanging a picture frame without tilting. ** Including all materials inside the frame, we simply list up a frame. We should omit the descriptions of material, color, shape, etc., if they are not essential in the analysis of their functions in the system. Some names representing concrete things, such as "a screw-eye", are replaced with generic words representing their principal functions, such as "a hook". |
** Instead of asking students to list all the objects they can think of, or all relevant objects, I usually ask for all the objects they think they need to understand the problem. I then ask them to reduce this to the minimum set needed to contain the problem. Many times, though not always, we reduce a seemingly complex problem to two, three, or four objects.

(9) At the end of the first stage of USIT process, i.e. the Problem Definition Stage, Sickafus confirms the focus of the problem, namely the essence of the problem defined. Whereas we are trying to improve our present system of the picture hanging kit, supporting the weight of the frame is not important but aligning the frame at the right position and angle is of the principal interest, namely the focus of the present problem. This recognition gives a direct influence on the analysis at the next stage, especially on the the analysis with the Closed-World Method. Failure in this recognition will lead you to an analysis out of focus. |

(10) The Second Stage for solving a problem in USIT is the stage of Problem Analysis. For this stage, USIT has two main analysis methods: one is the "Closed-World Method" for the approach of considering improvements from an existing system and the other is the "Particles Method" for the approach of making an image of an ideal solution first. The present case is analyzed by using the Closed-World Method. (The Particles Method is not explained in this article.) The first step of applying the Closed-World Method is to make a "Closed-World Diagram". This step intends to reveal principal functions among the minimal set of objects, which were listed up in Slide (8). USIT uses rather strict rules than other ordinary functional analysis methods and tries to represent the functional relations in a much focused way. This slide explains USIT's intention and its rules. |
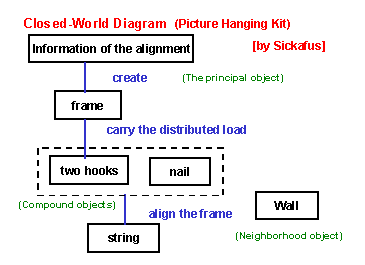
(11) This slide shows the USIT way of functional analysis, as drawn by Sickafus in the "Closed-World Diagram". The most important thing (object) in this picture hanging kit system for aligning the frame at the right position is the information how well the frame is aligned; thus it is placed at the top level. The "information" is regarded as a kind of objects in USIT; this treatment is especially useful for representing the systems for detection, measurement, and control. The information of alignment is generated directly by the frame. Thus the frame object is shown directly below the information object, and they are connected with a line showing the function. The load of the frame is born by the two hooks, then the hooks are hung by a string, and the string is supported by the nail for carrying the load. Considering that the function of the system is focused on the well alignment of the frame, Sickafus represents the system in such a way that the hooks and the nail form a compound object and the string provides the function to determine the alignment of the compound object. The wall is considered as a "neighboring object", because it is not controllable by the designer of the hit. |
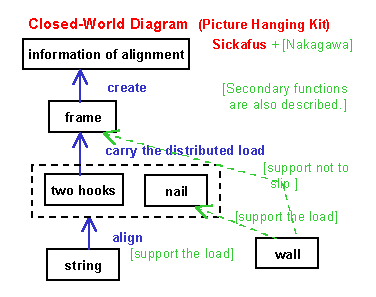
(12) As an extension of Sickafus' way of the "Closed-World Diagram", Nakagawa is now proposing to draw the diagram in a manner shown in this slide. Sickafus draws the diagram as concisely as possible in order to clarify the focus by omitting every non primary information. However, Nakagawa is now thinking that we should better represent some more functional information in this diagram for easier practice of using this diagram in the later stage of USIT. In particular, it is suggested to write subsidiary but important functions as well in the diagram, with enclosing them in the brackets [ ]. By writing subsidiary functions in [ ], we feel more comfortable to distinguishing the primary functions in the diagram. For instance, the function of carrying the load of the frame is the primary function in the ordinary sense for designing the picture hanging kit but is treated in the present analysis as the non primary function (thus omitted in Sickafus' diagram) and shown as such in the brackets in this Nakagawa's slide. It is suggested that the primary functions should be drawn with solid arrows while subsidiary functions with broken-line arrows. The arrow symbols are useful to select proper verbs for expressing the functions with distinguishing subjects and objects. By listing the subsidiary functions as well, the Closed-World Diagram becomes more useful in the Solution-Generation Stage of USIT to consider various ways of applying the Function Distribution Method. The functions to which we should apply the solution technique are already listed in this enhanced diagram. ** |
** I'm not convinced that this is true. To my way of thinking it is sufficient to consider only the most important functions of the intended design.I always remind each class that they already are capable problem-solving engineers and scientists. So USIT is not needed to do conventional engineering analyses. It is needed instead to help generate unusual perspectives of a problem and do it quickly. Small sets of objects, attributes, and functions already produce a lot to think about.
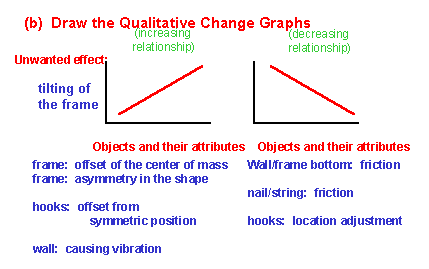
(13) Next step in the Closed-World Method is to draw the "Qualitative Change Graphs". The two graphs in this slide are, as a matter of fact, pre-fixed. The analyst needs to clarify the ordinates and the abscissa of these graphs. As the ordinate (of the both graphs), we should choose the unwanted effect in the problem. In this case, the tilting of the frame is chosen. (On the contrary, in some other cases, the desired performance of the system may be selected as the ordinate of the graphs. In such cases one should just interpret the graphs in the reverse way. ) ** As the abscissa of the graphs, we should list up the quantities which are in either increasing (i.e. in correlation) or decreasing (i.e. in anti-relation) relationship with the effect in the ordinate and show them in the form of the corresponding attributes of the objects. For example, as the increase in the offset of the center of mass of the frame, the tilting of the frame increases (in its most stable state); thus this attribute is listed under the left graph representing the correlationship. As is discussed in the next slide, Sickafus himself has improved bit by bit the way of drawing the Qualitative Change Graphs. This slide is drawn not in Sickafus' original form in the USIT textbook, but in a new way essentially following Sickafus' recent reference and further refined slightly. |
** I don't think I've ever used a desired effect (at least not in recent years) for a QC graph.

(14) When I made the previous slide (13) by following Sickafus' description, I realized that the slide was just drawing the mechanism of the problem (i.e. plausible root causes and possible factors for solutions). Instead of trying to list up as many attributes as possible in these graphs, Sickafus recently advises sure to list up the relevant attributes essential to the system in the problem. This shift in stress may be understood to confirm my observation mentioned above. Further more, I have recognized that Sickafus calls these graphs as "Plausible Root-Cause Graphs" in a recent article in his WWW site; I indeed agree with him in calling so. The description "How to use the Qualitative Change Graphs" should be noted. "To think of solutions in the direction to reduce the unwanted effect" is the most basic way. All the orthodox solutions in the engineering sense can be obtained in this direction. Thus, in practice in problem solving we should certainly consider in such a direction first. However, some problems may not be solved satisfactorily in this direction; then we should try the three other directions of thinking. All the three guide us to think the problem towards unusual and inventive solutions. [Sickafus notices here that some USIT seminar participants who learned TRIZ beforehand try to extract from these graphs "Technical Contradictions" in TRIZ sense and to solve them with TRIZ' Contradiction Matrix. He warns them that such a process is merely the waste of time. Indeed, I realize that the guidelines shown in this slide are much clearer to understand and useful in practice. ] |

(15) In the USIT Textbook (1977), Sickafus uses the "OAF Diagram" as the third step in the Closed-World Method. However, Nakagawa feels this OAF Diagram method is too complicated and unnecessary. (At the 3-day USIT Training Seminar in March 1999, Sickafus himself did not teach this method due to the limitation of time.) Nakagawa does not use this OAF Diagram for himself and regards it more reasonable not to teach them in his seminars. Thus, in this commentary, the description of the OAF Diagram is skipped. Sickafus claims: "When a function works between two objects, one attribute of each object supports the function. It is important for us to find which attribute of each object is involved in the function." And then he says: "If you obtain enough sense of distinguishing relevant attributes in the problem, you may safely skip this OAF Diagram." ** |
** When students seem to have difficulty with plausible root cause diagrams and QC graphs, I resort to OAF Diagrams to help them focus on attributes. Students have little difficulty dealing with objects and functions, but have a lot of difficulty using attributes effectively. This happens simply because attributes are an unfamiliar viewpoint to a problem. Thus, they need an instructor's guidance to discover how powerful is this perspective.
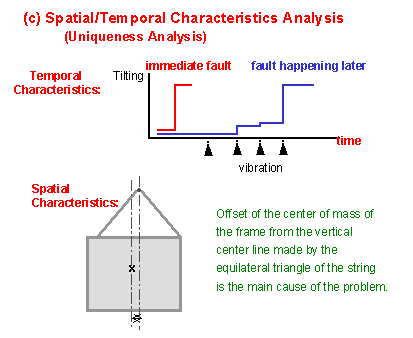
(16) In USIT, after the problem analysis with the Closed-World Method (and/or the Particles Method), is always applied the "Spatial/temporal Characteristics Analysis" Sickafus calls this method simply as "Uniqueness". The aim of this method is to examine any unique characteristics of the system with respect to space and time and then to think of any solution getting favor of such unique characteristics. Typical way of description in this analysis is shown in the graph of system's temporal behavior in this slide. The unwanted effect is taken along the ordinate while some characteristic time axis is taken along the abscissa; thus the graph shows the temporal behavior of the system in problem. This slide illustrates two cases; a case when the frame gets tilted immediately after being hung, and another case when the frame tilts little by little with some impacts and then suddenly gets tilted to the most stable position. The description of the spatial characteristics in this slide is not so typical but illustrates the spatial drawing of the system and explains one principal plausible root cause. [It is important to analyze the system's characteristics in space and time and illustrate them to reveal their uniqueness; the format of the drawings may be modified and adapted for each case of the problem. To show the temporal behavior, the process analysis of the system may sometimes be most powerful.] ** |
** Toru, I did not realize, until reading your text and going back to my book, that no good graphics are given in the book for uniqueness. There is only the suggested graph shown in Fig. 10.1 (which I now don't like). Since writing the book, I now place much more emphasis on Uniqueness as a problem solving method and spend some time generating the appropriate (but simpler) graphics.I do not address first the unwanted effect in uniqueness diagrams. Rather I emphasize first when and where desired functions are active. Hence, the spatial diagram of uniqueness often is the original object-object interaction sketch. It shows where the objects are in space and where their points of interaction support specific functions (your slide (3), for example.). However, I as the instructor must go back to this drawing and call attention to these aspects for the students. I then do a temporal drawing with no label on the ordinate. Time is the variable on the abscissa. I then add simple rectangles, each labeled as a desired function. This graphic illustrates clearly when functions are on or off, when they overlap and don't overlap, when they are multiplexed and when they are not. Each of these points is the start of the associated thinking process for generating new solutions. Once constructed, it may be useful to address the unwanted effect from the viewpoint of temporal and spatial uniqueness.
Students often discover uniqueness aspects of a problem without considering spatial and temporal effects, and this is good. I introduced temporal and spatial uniqueness diagrams as a tool for the many students who have trouble with the concept of uniqueness. It has been very successful, but it is not the only approach.

(17) The Problem Analysis Stage having finished, we now start the third stage of USIT process, i.e. the Solution Generation Stage. It is not easy to explain the process of solution generation. Some solutions may be obtained by logical applications of appropriate solution techniques, but most solutions may come out (or actually came out) while thinking the problem in various ways and in various contexts. Thus, if we write the solutions in the actual order of their coming out in our mind, the solution process may seem to jump this way and that way in the logical space. On the other hand, if we explain the solutions in some logical order, some of the readers may become suspicious of such logical explanation of the solution generation process. Thus, you should better understand that the solutions explained here are presented as a summary of thinking in different ways and of repeated reviewing. Among the five ways of solution generation in Sickafus' explanation in this slide, (a) and (b) are extension of idea generation on the basis of the analyses obtained so far. On the other hand, (c), (d) and (e) are the solution generation with the use of principal three solution-generation techniques in USIT. (Note: Sickafus calls the three solution generation methods in (c), (d) and (e) simply as "Dimensionality", "Distribution" and "Pluralization"; but Nakagawa uses (in Japanese) their full names as "Attribute Dimensionality Method", "Function Distribution Method" and "Object Pluralization Method". So the latter names are used in this article.) ** In the following slides, I have rearranged the solutions in the order I feel most smooth in logic. Each solution is illustrated in a slide in a uniform style. The process of thinking is mostly described in the commentary part (i.e. in the right column). |
** I like your more complete titles for the solution techniques.

(18) At the starting point of the solution generation stage, we notice that in the analyses of the problem mechanism and plausible root causes the "offset of the center of mass of the frame" is found most important. Thus, we should first think of methods to eliminate such an offset. "We should better eliminate the offset of the center of mass of the frame in the manufacturing process"; this is a sound and obvious approach to solving the present problem. When we think about this solution concept more closely, we easily notice there are a number of factors we can and should control in the manufacturing process in the factory but some more factors which depend on the customers' handling of the frame and the pictures. Thus we have added some detailed solutions to guide the customers to handle the frame properly as the part of solutions manufacturers must take care of. [At the bottom of each slide, the solution is reviewed from the point of application of the solution generation techniques. In this solution, the attribute of the offset of the center of mass of the frame is tried to be fixed to the zero value; thus we may say the Attribute Dimensionality method is applied. In other sense, the adjusting function is tried to move from the customers' handling process to the manufacturing process in the factory; this may be interpreted as an application of the Function Distribution Method. It is often the case that a solution can be explained in multiple views of applying the solution generation techniques.] |
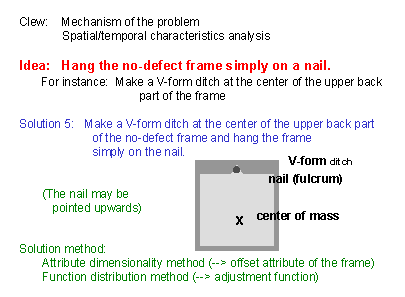
(19) In the previous solution, we have produced "no-defect frames without offset of the center of mass". Hence, we do not need any further adjustment by the customers for aligning the frame. So we may quit using the 3-point suspension system which was introduced for the alignment function, and can just hang the no-defect frame simply on a nail without tilting. Noticing this consequence, the idea is written down in this slide. If we think of the suspension system always with a string, simple ideas like this one are not easy to be noticed. Thinking of the functions and purposes of the system and its components should be useful for recognizing this kind of simple yet useful ideas. For hanging the no-defect frame simply on a nail, we should better have some mark at the right position for hanging, and some mechanism for getting the frame hung naturally at the right position. Thus we have obtained the solution of making a V-formed ditch at the right place, as shown in this slide. The nail may be a simple cylindrical shape. (If the head of the nail fits into the inside of the V-shaped ditch, the frame will become safer because of not coming out frontward.) |
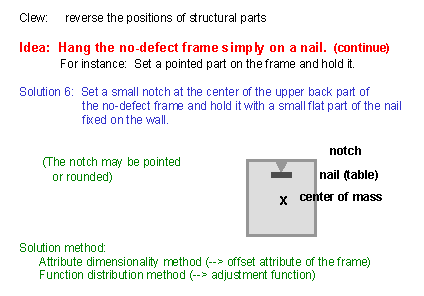
(20) There may be another idea of mechanism for hanging the frame simply. We may make a small notch, in place of a ditch, at the upper back part of the frame and put the notch on a table-like part of the wall-fixed nail. This is an idea where the mechanism of the previous solution is partially turned upside down. A notch sharpened downwards may be easier to think of, as illustrated in this slide. However, a sharp edge is not necessary; cylindrical or hemispherical notches will also work. |
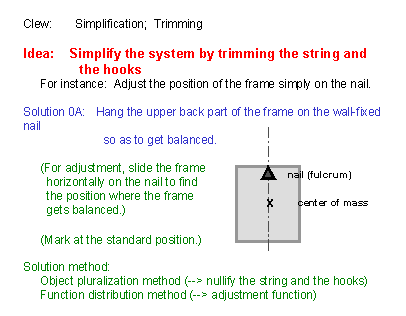
(21) On the basis of the previous ideas for simply hanging the no-defect frames, we would like to figure out some simple method for hanging actual frames having slight offsets of the center of mass. We may say we come back from the ideal case to real situations. This slide shows an idea for hanging the real frame on a nail as simply as the two previous slides. Here we use no hooks and no string; we may say we have trimmed the two hooks and the string from the original 3-point hanging system. Actually, we should fix a nail on the wall and put the upper back rail of the frame on the nail and try to find the balanced position by sliding the frame horizontally. (Since the frame is not the no-defect one, the balanced position may be off the center of the upper rail but it may be easily found near the center. A mark at the center may be of some help.) [The trimming technique belongs to the Object Pluralization Method. Zero is a kind of plural (in English). Trimming is a typical way of "Simplification".] |
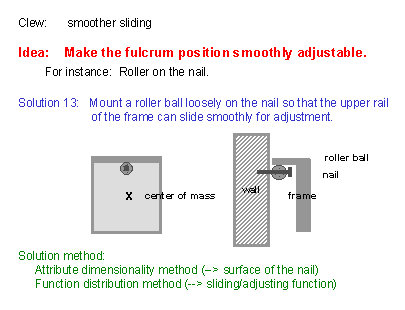
(22) In the previous solution, the frame is adjusted to find its balanced position by sliding its upper rail on the nail. Thus it may be helpful to make the frame smoothly slidable on the nail. This suggests the use of a wheel. A small wheel may be set on the nail, by using the nail as the wheel axis. The idea shown in this slide uses, in place of a wheel, a solid ball rollable around the nail axis. (When we think to support something at a point, we often imagine a pointed edge and apt to fail in thinking of rounded edge like this one. We should always be careful to broaden our way of thinking.) [As for the solution generation technique, considering the change from the previous slide (21), we have tried to reduce the value of the friction attribute of the nail surface; this means we have applied the Attribute Dimensionality Method. In another view, we have thought of the adjusting function and realized it by the sliding function of the frame on the nail; thus we have applied the Function Distribution Method. ] |
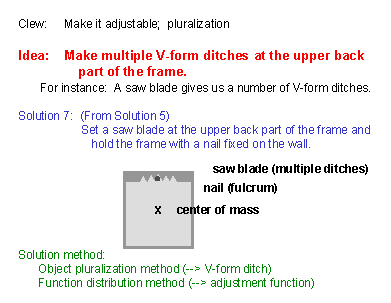
(23) In the solution of slide (19), we have made a ditch at the center of the upper part of the "no-defect" frame. For real frames, which may have slight offset of the center of mass, we may think of providing multiple ditches around the center position. If we make a number of V-formed ditches, they look like a saw blade. (It should be another story whether we use the saw blades in market for this purpose.) [Since we have multiplied the V-formed ditch, we may say we have applied the Object Pluralization Method as the solution generation technique. (Note: Rigorously speaking, the ditch itself is regarded in USIT not as an object but as an attribute of the frame object. But here we may handle the ditch as if it were an object.) In another view, we may think that we have applied the Function Distribution Method to install the adjustment function into the single-ditch solution.] |
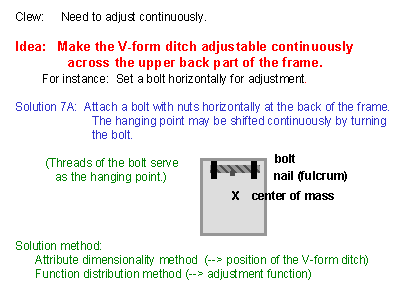
(24) In the above solution with a saw blade, the number and the position of the ditches are fixed; thus there can be a problem that there is no ditch at the right balanced position. Thus we would like to install the continuous-ajdustment function. It may be an idea to make the ditch slidable horizontally and hold the ditch with a screw at the balanced position. This slide shows a sophisticated solution given by Sickafus; a bolt is set horizontally with two nuts and turned for adjusting. (It is a merit that the direction of the load of the frame is perpendicular to the direction of turning for adjustment of tilting. ) [This solution may be regarded as an application of the Attribute Dimensionality Method in the sense that we made the position attribute of the ditch variable. We may also say that we have applied the Function Distribution Method because we installed the continuous-adjustment function.] |
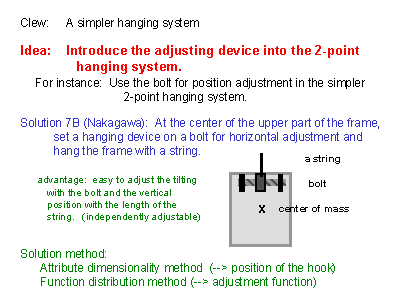
(25) In the previous solution, we provide a mechanism for horizontal adjustment and hang the frame directly on a nail. We may have another solution here; we may hang such a frame having a horizontal adjustment mechanism with a string. This slide shows such a new idea inserted by Nakagawa. This corresponds to the idea that I obtained while thinking of the improvement of the two-point suspension system as mentioned in Slide (6), and enhances the two-point hanging system by introducing a mechanism for adjusting the hanging position. This solution has a unique merit which has not been discussed so far. In this mechanism the length of the string may be changed easily for adjusting the vertical position (or the forward tilting angle) of the frame, independently of the adjustment of tilting in the frame plane. As you know, such vertical adjustment is rather difficult to achieve by changing the string length in the 3-point hanging system. [The applied solution-generation methods are shown in the slide from the view point of generating this solution from the 2-point hanging system.] |

(26) Let us go back to examine the results of the problem analyses again. We now recall that the relationship between the wall and the frame has been mentioned several times. So we should first think of the problem caused by the vibrational impacts from the wall. This problem was illustrated clearly in Slide (16) in the temporal characteristics analysis. In order to reduce the vibrational impacts from the wall, we may readily think of a solution to use some cushions. Now, in addition to the materials like sponges and rubbers, we should better expand our associative thinking for seeking for various type of materials and interactions. On the basis of the keyword "elastomeric", we may find "adhesive" and "cohesive", etc.; such keywords may be useful later. This way of extending the ideas by using generic words and associative thinking is encouraged in USIT as the "Generification Method". [We may think that we have added a new attribute of elastomicity of the surface of the wall (or of the lower edge of the frame). We may also think that we have improved the tilt-suppressing function of the wall (due to the friction) and introduced the function of damping the vibrational impacts.] |

(27) The friction between the bottom part of the frame and the wall is not a principal but an important subsidiary function for holding the frame at the desired position. If these subsidiary functions are shown in the (enhanced) Closed-World Diagram, as in Slide (12), they are useful for us to consider various solution concepts, especially by applying the Function Distribution Method. For further stability of the frame, we should better increase the friction at this part. We are encouraged to create images of solutions in such a direction and to enhance them further. Coming over the boundary of the concept of the friction, we should think of new concepts such as adhesion, cohesion, attractive force, combining, etc. in an associative way. (This way of thinking both in concreteness and in abstract is a basic feature in TRIZ and is encouraged much in USIT. Such a way of thinking is certainly important for writing patent applications.) |

(28) When we analyzed the mechanism of the problem in Slide (6), we found that at the instance when the frame gets tilted to the most stable position, the string slips on the nail. If it is the case, we may be able to prevent the frame from getting tilted by increasing the friction between the string and the nail. This is the idea shown in this slide. We may easily obtain ideas such as to make the surface of the nail rough, to use some string material having larger friction coefficients, etc. When we think of other kinds of work where strings are used (such as binding things together with a string, holding a boat with a rope, etc.), we may have an idea of winding the string around the nail. This is a very effective way to increase the friction between the string and the nail. (As the function of the nail, we notice the load-carrying function easily but not so much the subsidiary function of holding the string with the friction. By noticing such a subsidiary function, we can get a new type of solutions, as you see in this slide.) |

(29) If we wind the string around the nail, there arises a difficulty: While the string is not tight, we wind the string around the nail and adjust the position of the frame, and then set the frame by making the string tight. However, we often find the frame is set tilted slightly, and have to readjust the string position by loosening the whole string again. This subsidiary problem is due to the difficulty of making the adjustment function compatible with the friction-holding function. This difficulty in compatibility may have a focus on the friction attribute of the nail. For adjusting, the friction is requested to be small, whereas for holding it is requested to be large. This pattern of conflict is exactly the "Physical Contradiction" in the TRIZ theory. For solving this kind of conflict, TRIZ teaches us to separate the two opposite requests with respect to time or space. This slide shows the solution by Sickafus. The two requests are separated in two different parts of a nail (i.e. separated in space), and further separated in two different time periods of usage, i.e. during adjustment and afterwards (i.e. separated in space, as well). [As for the solution generation methods, we may regard that a smooth surface nail and a rough surface nail are joint to form this compound nail, and hence that we have applied the Object Pluralization Method to the nail.] |

(30) In Slides (26) and (27), we have had an idea of applying some adhesive material between the wall and the bottom part of the frame. Then, we may think of a more drastic idea to apply such an adhesive between the wall and the whole part of the frame. Sickafus encourages us to use this sort of ideas and further enhance them into "metaphors", such as a "sticky wall" in this case. "Metaphors" may be understood here as generified conceptual solutions having loose and wide meaning spoken in everyday words (or images). From specific and concrete ideas, we should try to obtain their metaphors as templates for new ideas; this is the aim of the "Generification" Method in USIT. In this metaphor of "sticky wall", we should imagine a wall which sticks the frame but lets it go whenever necessary, instead of a wall which fixes the frame forever. [In the sense of functional analysis, we may say we are redistributing the load-supporting and position-holding functions in a drastic way.] |
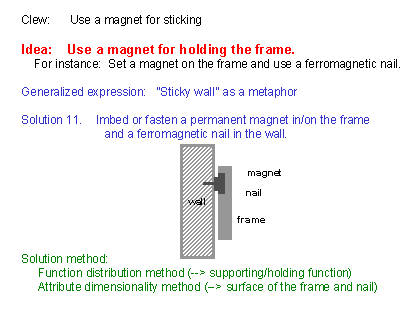
(31) One of the method to get the frame stuck is to use a magnet. In this slide, the idea of hanging the frame with a nail still remains in our mind; hence we are applying the magnet between the nail and a part of the frame. We imbed a magnet in the upper back part of the frame and use a ferromagnetic nail so as to be attracted by the magnet. Slight adjustment of the vertical/horizontal positions and the tilting angle can be easily achieved with this magnetic interaction. (There may be a weak point in this idea; the magnet may not provide enough fixing and load-supporting strength. It may be practical to combine this idea with the conventional ways of supporting the load.) [As for the solution generation methods, we have introduced a new property of magnetism into the nail and the frame; this is the typical way of "extending the dimension of attributes of the objects" or of "activating an attribute" in the Attribute Dimensionality Method in USIT. |
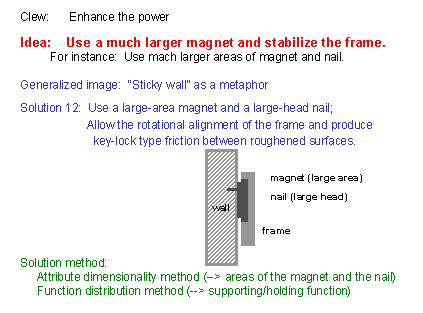
(32) We have an idea of enhancing the previous solution by increasing the area of the magnet and make the hold more stable. On the wall we fix not a nail but rather a large-area board of ferromagnetic property. The magnet should work over the large area of the board and should hold the frame with enough power. [As the attributes of the nail, we have introduced not only the ferromagnetism attribute but also the nail-top area attribute to actively use in the solution. So, this is a typical way of "activating new attributes" in the Attribute Dimensionality Method.] |
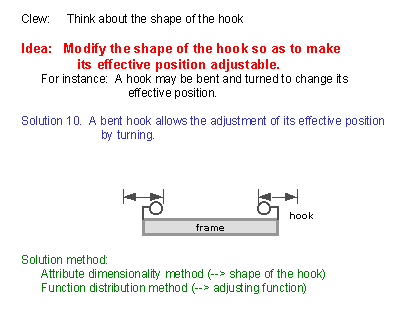
(33) Now let us go back to the discussion of the mechanism of the problem again. We recall that the positions of the hooks are important especially with respect to the position of the center of mass of the frame and in the point whether the hooks are located symmetrically. Then we may notice that we should be able to adjust the position of the hook(s). The idea in this slide proposes to bend the stem of the hook in the L-shape and to adjust its effective position by rotating the hook. (In this solution, the screw part for fixing the hook is assigned to carry two functions, namely the screwing-in function for fixing the hook and the angle-adjustment function for setting the effective position of the hook. Thus, if we use a simple bent screw in this solution, the hook may have the flaw of getting loose easily. We should better use a bolt and a nut for separating the adjustment and the fixing functions.) The idea in Slide (25) may also be used for the adjustment of the hook position. |
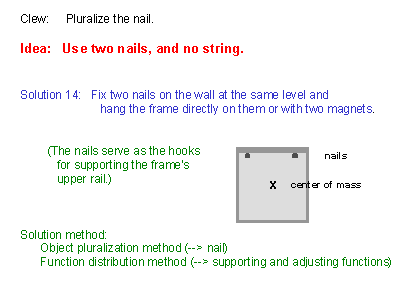
(34) This solution has been obtained by applying the Object Pluralization Method intently. While trying to hang the frame simply on a nail (i.e. as in Slides (19)-(21)), we had a idea to use two nails simultaneously. It is usually not so difficult to fix two nails on the wall at the same height (or at the same horizontal level). Since we have set the level line with these two nails, we should just hang the frame directly on the nails. (We may have a number of concrete ways of such hanging, as shown in some examples in this slide.) It may be difficult to think of this solution directly from the original system (composed of a nail, two hooks, and a string). But you may come over to this idea with several steps of jumping. Such a path of getting at this idea can be quite different from one person to another. |
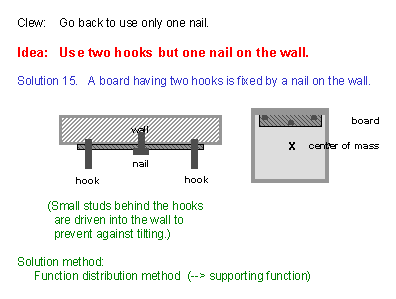
(35) This is a much sophisticated solution. This solution can come up with only on the basis of the preceding idea (Slide (34)). The preceding idea of using two nails is a simple and good solution, but has a weak point of the necessity of driving two nails into the wall. (Though this weak point is not serious, there can be always somebody who claims.) Hence, we tried to return to use only one nail but to keep the advantage of using two supports (or hooks) in the preceding idea; such a trial has brought Sickafus this solution. We are thinking to fix a board having two hooks by driving only one nail on the wall. The nail is supposed to be able to carry the load of the frame but not to be able to resist the torque in case of uneven weight. Thus, behind the two hooks small notches are attached and are set slightly into the wall for preventing the tilting of the board. This is a nice, sophisticated idea by Sickafus. [This idea may be obtained by thinking the distribution of various functions to the parts of the system; thus we may say the Function Distribution Method is applied for obtaining this idea.] |
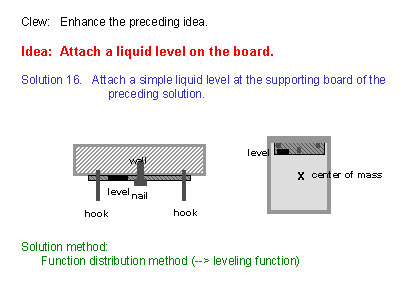
(36) If we think of our procedure for setting the device of the preceding solution (Slide (35)) on the wall, we would drive the nail into the wall while checking the board is set horizontally (i.e. two hooks at the same level). With this thinking, it is quite natural for us to introduce a function for checking the level of the board having the two hooks. Thus we get an idea of attaching an inexpensive liquid level device, as shown in this slide. [The new function for confirming the horizontal level has been introduced in this solution; this is a typical way of applying the Function Distribution Method.] |
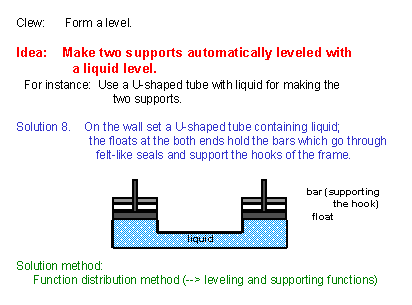
(37) We may enhance the preceding idea of using a liquid level device to create an automatically maintained level of the hooks. As a method to keep two points in the same horizontal level, we may easily think of a connected tube. Then, we make a device like a piston at the each end of the U-shaped tube containing a liquid, and let it support each of the two points of the frame, as shown in this slide. (Various examinations whether this sophisticated device works properly, whether it is cost-effective, etc. should be made only after producing as many new ideas as possible with USIT. In the process of USIT, the problem solving team is advised to think of as large a variety of ideas as possible and write them down as alternative conceptual solutions.) [Since we have combined the functions for creating the level and for supporting the hooks, we may say this is an application of the Function Distribution Method.] |
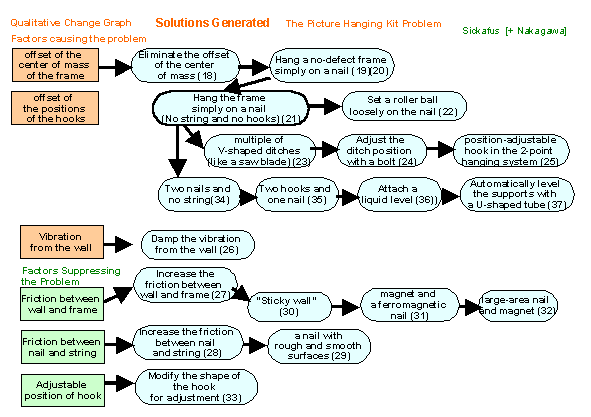
(38) As a summary of the Solution Generation Stage in USIT, Nakagawa has made this slide for overviewing the relations among the solution concepts obtained so far. In the left-most column, the attributes which were listed in the Qualitative Change Graphs (Slide (13)) are shown in rectangles; they are grouped into the factors causing the problem and the factors suppressing the problem, corresponding to their increasing/decreasing relationship to the effect of the problem. You may clearly notice that various solution concepts have been created through the consideration of these factors causing/suppressing the problem. A large number of solution concepts are shown in the round-corner rectangles. The numbers in ( ) represent the slides in this article. You may notice that some simple ideas form the bases for generating many more solutions. Sickafus encourages to form these simple ideas as "metaphors". Elaborated and sophisticated solutions are shown towards the right in this slide. The arrows among the solutions (and the factors) represent some logical paths in reasoning, according to Nakagawa's sense. However, the actual history of solution generation may often be quite different from this kind of logical path. It should be remarkable that USIT has generated all these multiple conceptual solutions smoothly and systematically. In TRIZ (or in most of TRIZ textbooks), single innovative solution is usually sought for each problem. But USIT sets, in its philosophy, a different goal as illustrated here. |

(39) This slide lists all the solution generation methods in USIT, as a review. For generating a multiple number of conceptual solutions, Sickafus advises to apply the four techniques from (a) to (d) repeatedly and to generify the solutions further with the method (e). By giving a 3-day USIT Training Seminar during July 11-13, and further by preparing these slides and writing this article, I feel I learned the meanings of these solution generation methods more deeply. For obtaining each solution concept, we may have different paths and we may apply not only one but multiple solution-generation techniques. Though this point was mentioned by Sickafus, I really understand it only after I write and revise these slides. Furthermore, I am thinking of one more improvement in USIT. I now feel that if we slightly change the position of the method (d), USIT would become more convincing and useful. According to the principle of USIT, it would be more natural to regard the three methods (a), (b) and (c) as the principal techniques for solution generation rather than to regard the four including (d). Corresponding to the USIT's three basic concepts (i.e. Objects, Attributes, and Functions), USIT provides three solution-generation techniques which focus and operate on each of the three basic concepts. |
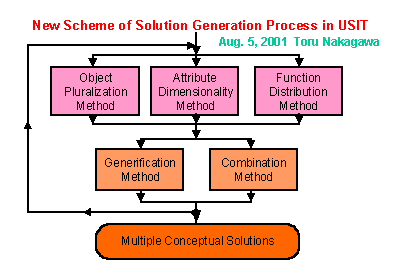
(40) This slide shows the possible new scheme for the solution generation stage in USIT. From the former standard scheme, the Transduction Method (d) is enhanced and renamed as the "Combination Method", and moved to the position in parallel to the "Generification Method", as shown in this slide. (Speaking more logically, the last two methods should be called "Concept Combination Method" and "Concept Generification Method".) The "Combination Method" stands for a variety of methods to combine elements of different solutions. Sequential use of functions (i.e. the Transduction Method) is just one type of combination. We may also include parallel use, switching, compromise, hybridization, convolution, nesting, reverse use, etc. of two (or more) functions or elements of ideas. Thus in this new scheme, the three solution generation techniques are applied to objects, attributes, and functions, respectively to generate conceptual solutions (or their elements) and then the two methods are applied further to such concepts for generifying and combining them. By using these five methods repeatedly, we are sure to be able to obtain multiple number of conceptual solutions. ** |
** I've considered other flow-chart organizations for the solution techniques also. However, I'm not ready yet to commit to any because I have not seen enough new solutions to be convinced that it would be useful. The big problem with flow charts is how structure cues the mind.As described so far in this article, I studied this Sickafus' textbook problem closely again and explained it with my own words; this work was very fruitful for me. The philosophy and techniques of USIT's way of problem solving have been revealed much for myself through this work. Some parts of my explanations of USIT so far seem to be restricted and dependent on my experiences. I have realized again that it is important for us to study textbook examples and real case studies and applications closely, and to apply the problem solving methods dynamically and flexibly depending on the real cases. **
** You've convinced me that your effort in producing a slide presentation on the picture hanging problem has benefited your understanding of USIT. In my opinion, the two most important exercises for a USIT train-the-trainer class is preparing all of the slides for a problem-solving demonstration and doing a reverse engineering exercise (such as the Sicilian Dolly example on my web site).
| Top of this page | 1. Problem Definition | 2. Problem Analysis | 3. Solution Generation | Introduction to USIT (Nakagawa, Apr. 2000) | Japanese
page |
| Home Page | New Information | Introduction to TRIZ | TRIZ References | TRIZ Links |
| TRIZ News & Activities | TRIZ Software Tools | TRIZ Papers and Tech Reports | TRIZ Forum |
Last updated on Aug. 23, 2001. Access point: Editor: nakagawa@utc.osaka-gu.ac.jp